상관분석
상관계수
데이터: 두 연속 변량(X, Y)에 대한 자료가$(x_1, y_1), (x_2, y_2), ..., (x_n, y_n)$
독립변수(설명변수)x에 대하여 종속변수(반응변수)y의 값을 관측 -> 데이터가 pair로 얻어진다.
표본상관계수의 성질
- 표본상관계수는 X와 Y 사이에 어느 정도 직선 관계가 있는지를 나타냄.
- $-1 \leq r \leq 1$
- r < 0이면, 양의 상관관계, X의 값이 커짐에 따라 y값도 커지는 경향이 있다.
- r < 0이면, 음의 상관관계, x의 값이 커짐에 따라 y의 값을 작아지는 경향
- r = +=이면, 모든 점은 직선 위에 있다.
무상관(無相關)
r = 0일 때, 상관관계가 없다는 뜻은 두 변량 X, Y사이에 선형관계가 없음을 뜻한다.
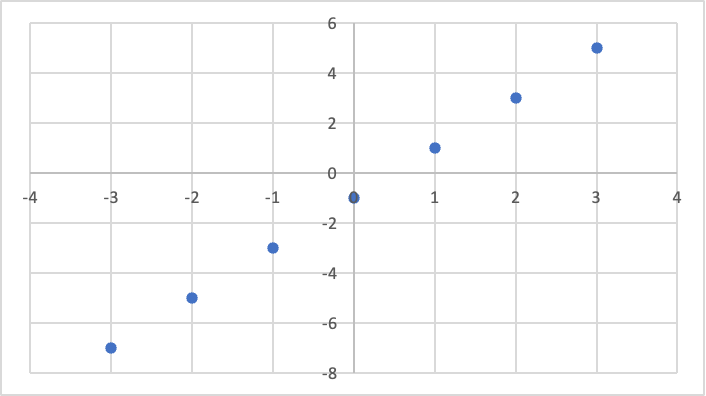

이차식의 관계가 있음에도 상관계수의 값은 0
무상관 검정
가설 설정:$H_0: p = 0 || H_1: p \neq 0$
검정통계량: 자유도가 n-2인 t분포$t_0 = r\frac{\sqrt n-2}{\sqrt 1-r^2} \sim t(n-2)$
임계값:$H_1: p > 0: Reject H_0 if |t_0| > t_a/2(n-2)$
상관계수 구하는법
| X | Y | $x-x_m$ | $y-y_m$ | $x-x_m^2$ | $y-y_m^2$ | $x-x_m*y-y_m$ |
상관계수 correl() = $(x-x_m)*(y-y_m)/\sqrt(x-x_m)^2 / \sqrt(y-y_m)^2$
상관분석 가설검정
가설(양쪽검정): $H_0:p = 0 H_1:p \neq 0$
검정통계량:$t_0 = r \sqrt \frac{n-2}{1-r^2}$
자유도 = n-2, t분포
p-value = T.DIST.2T(검정통계량, 자유도)
임계값 = T.INV.2T(유의수준, 자유도)
회귀분석(regression)
설명변수와 반응변수
| 설명변수(독립변수) | 두 변수 중 다른 변수에 영향을 주는 변수 |
| 반응변수(종속변수) | 설명변수의 영향을 받는 변수 |
독립변수(x)와 종속변수(y) 사이에 Y = f(x)의 함수관계를 찾고, 종속변수의 값을 예측하기 위한 모델링
함수형태로 주어지는 직선 또는 곡선을 회귀방정식이라고 한다.
- 단순회귀분석: 독립변수가 1개 일 때
- 다중회귀분석: 독립변수가 2개 이상일 때
단순선형회귀분석
독립변수가 1개, 독립변수 x와 종속변수 y사이의 선형관계 Y = a +bX
데이터: $(x_1, y_1), (x_2, y_2), ..., (x_n, y_n)$
단순선형회귀모형: $y_i = a + bx_i + \epsilon _i, \epsilon _i는 오차항$
회귀직선과 오차

회귀분석에서 오차에 대한 가정
회귀모형에서 오차항은 다음을 가정한다.
- 독립성: 오차항은 서로 독립적이다.
- 등분산성: 분산이 동일하다.
- 정규성: 정규분포 $N(0, \sigma^2$를 따른다.
모수(기울기와 y절편)의 추정
회귀모형:$$y_i = a + bx_i + \epsilon _i$
오차항:$\epsilon _i = y_i - (a + bx_i)$, 오차항의 합은 0
오차항의 제곱합을 최소화 -> 일명 최소제곱법 사용
최소제곱법
기울기:$\hat b = \frac{\sum \sum (x - \bar x)(y -\bar y)}{\sum (x - \bar x)^2}$
y절편:$\hat a = \hat y - \hat b \bar x$
회귀직선의 방정식은$\hat a = \hat y - \hat b x$
예측치: 설명변수 값이 $x_i$일 때, 회귀직선 위의 값을 예측치라고 한다.$\hat y_i = \hat \beta _0 + \hat \beta_1 x_i$
결정계수$(R^2)$
$(R^2)$ = 회귀제곱합/총 제곱합
결정계수가 1에 가까울수록 모형이 적합(오차가 적어진다.) 결정계수는 상관계수의 제곱과 같다.
다중 상관계수^2 = 결정계수$(R^2)$
예측치와 잔차

관측치: $y_1, y_2, ..., y_n$
예측치:$\hat y_1, \hat y_2, ..., \hat y_n$
회귀모형:$\hat y_1 = \hat a + \hat b x_i$즉, 예측치는 회귀직선 위의 값
잔차:$\hat e_i = y_i - \hat y_i$
회귀분석 방법
[데이터 분석] 메뉴에서 회귀분석을 선택하고 y, x축 범위를 지정한 후, 잔차, 잔차도, 선 적합도 클릭한 후 출력한다.
예측치
=forecast.linear(구하려는 값x, Y절편, x배열)함수를 이용해 푼다.
비선형회귀분석
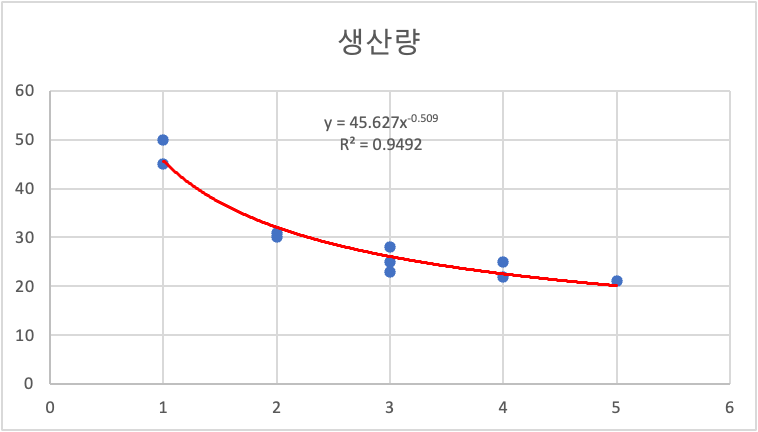
산점도의 형태가 직선으로 보기 어려움. 선형계수는 -0.87로 직선의 관계가 깊은 것으로 보임.
거듭제곱 추세선을 추가하면 결정계수가 0.94로 증가한다.
'전산통계 > 강의노트' 카테고리의 다른 글
| chapter9 - 범주형 자료분석(교차분석) (0) | 2023.06.04 |
|---|---|
| chapter 8 - 분산분석 (0) | 2023.06.03 |
| chapter 7 - 가설검정 (0) | 2023.06.03 |
| chapter 6 - 통계적 추정 (0) | 2023.05.17 |



